关于3D坐标变换的数学原理

        3D坐标变换被广泛应用，在机器人导航和器械臂控制上我们常常需要变换坐标系，参杂平移和旋转，本文对相关的数学原理做一个梳理。

（1）为了便于理解，首先从1维开始探讨。

）））人在车上走，车在地面上行驶。人相对于地面的速度 = 人相对于车的速度+车相对于地面的速度 ：

图1：一维坐标变换图示

（2）二维坐标变换的简单情况——只有平移：

）））向量(A), 在S1坐标系中有坐标（xa_s1, ya_s1）, S1坐标系原点相对于S2坐标系的坐标是(xs1_s2, ys1_s2)。 我们要得到(A)在S2中的坐标(xa_s2,ya_s2)，有：

））））））））                      xa_s2 = xa_s1 + xs1_s2;

））））））））                      ya_s2 = ya_s1 + ys1_s2.

            这里可以看成是在 (xa_s1, ya_s1) 引入一个平移变换(xs1_s2, ys1_s2), 这个平移就相当于一维例子中“车相对于地面的速度”。

（配图2：二维坐标平移变换图示）

（3）二维坐标变换的一般情况——平移和旋转：

）））向量(A), 在S1坐标系中有坐标（xa_s1, ya_s1）， S1坐标系原点相对于S2坐标系的坐标是(xs1_s2, ys1_s2)，S1坐标系相对于S2坐标系的旋转角是θ, (逆时针为正方向) 。 我们要得到(A)在S2中的坐标(xa_s2,ya_s2)，分两步完成：

图3：二维坐标一般变换，平移和旋转图示

            第一步： 旋转，使用欧拉旋转矩阵R(θ) = [ cos(θ)    -sin(θ)   ;   sin(θ)    cos(θ)]：

                             [ x_1 ; y_1 ] = [ cos(θ)    -sin(θ)   ;   sin(θ)    cos(θ)] * [xa_s1, ya_s1] .

                             此处矩阵乘法。用MATLAB中的协议表示一个矩阵，分号代表提行。

            第二步： 平移， 如上述：

                             [ xa_s2  ;  ya_s2 ] =  [ x_1 ; y_1 ] + [xs1_s2; ys1_s2].

                             得到(A)在S2中的坐标(xa_s2,ya_s2)。

            这里可以看成是在 (xa_s1, ya_s1) 引入一个旋转变换，再引入一个平移变换。这两个变换就相当于一维例子中“车相对于地面的速度”。具体过程如下图所示：

            我们可以把上述二步综合在一个变换矩阵中。如下图4，图中R(θ) 就是上述欧拉旋转矩阵，x_off = xs1_s2, y_off = ys1_s2. x = xa_s1, y = ya_s1, x’ = xa_s2 , y ’ = ya_s2。 把A在S1中的坐标变换为A在S2中的坐标（2D）:

图4：二维坐标变换的矩阵形式

            有了二维变换的基础，加上三维欧拉旋转矩阵的旋转角定义和矩阵内容，接下来讨论3D坐标变换的原理。

（4）三维欧拉旋转矩阵的旋转角定义和矩阵内容：

            此处讨论三维坐标采用右手定则。

            此处讨论的旋转角使用航空飞行领域常用的，pitch, yaw 和 roll 旋转。关于右手笛卡尔坐标系的绕 x , y 和 z 轴的旋转分别叫做 pitch, yaw 和 roll 旋转。

            参考： 1.  关于旋转角pitch,yaw and roll 的定义

                        2. 关于旋转角pitch, yaw and roll 的正方向的定义：与x轴正方向面对面，逆时针方向旋转为pitch正方向。yaw, roll 同理。

                            =============
                            如果有一个人站在零点，面向X轴正向，头顶向上方向为Y轴正向，右手方向为Z轴正向，那么旋转角度和方向的计算方法如下：
                            Yaw是围绕Y轴旋转，站在零点的人脚下是XOZ平面，以正角度为参数是向左转，以负角度为参数是向右转。
                            Pitch是围绕X轴旋转，站在零点的人脚下是XOY平面，以正角度为参数是向右倒，以负角度为参数是向左倒。
                            Roll是围绕Z轴旋转，站在零点的人脚下是YOZ平面，以正角度为参数是向后倒，以负角度为参数是向前倒。

                            =============

（5）欧拉三维旋转矩阵：

             此处使用的旋转矩阵是基于上述第（4）条旋转角定义的。一定要同步使用，吻合，才不会出错。

     下面图中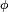， ,  and  分别代表pitch，yaw 和 roll. 

              The axes of the rotation depend on the specific convention being used. For the x-convention the rotations are about the ,  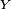and 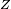 axes with angles 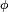,  and , the individual matrices are as follows:

This yields合计起来：

             有了这个数学的基础，我们再来完成3维的坐标旋转+平移就不是问题了：

把A在S1中的坐标变换为A在S2中的坐标:

         x, y, z 为A在S1的坐标，θ 为S1相对于S2 的旋转角，R(θ) 为旋转矩阵，x_off, y_off, z_off, 分别为从S2原点平移到S1原点的向量的三个坐标。x’ , y’, z’ 为A在S2的坐标。所以上述矩阵的乘法实际上是实现了把A在S1中的坐标变换为A在S2中的坐标。 S1相对于S2有旋转和平移。

参考：Rotation formalisms in three dimensions （ http://en.wikipedia.org/wiki/Rotation_formalisms_in_three_dimensions ）

我们可以看一个实例：

 旋转角： *α

*

*Ya_o2 = L2 cosα cosβ -  L2 sinα sinβ + L1 cosα*

*Za_o2 = L2 sinα cosβ +  L2 cosα sinβ + L1 sinα*

上一个例子的MATLAB计算及演示程序如下：

% 我们假设alpha值在 π/6 到 2π/3, beta值在-2π/3 到 -π/6
% L1 = 348; L2=400
% 这个程序通过画图展示了串联机器人的坐标运动范围。
 alpha = [3.1416/6: 0.01: 2*3.1416/3];
 beta = [-2*3.1416/3: 0.01: -3.1416/6];
 L1=348;
 L2=400;
 cosA=cos(alpha);
 cosB=cos(beta);
 sinA=sin(alpha);
 sinB=sin(beta);
 cosA = cosA';  %这里是矩阵转置
 sinA = sinA';
 len = length(cosB);
 One = ones(1,len);  %全为1的单行矩阵
 Ya_o2 = L2*cosA*cosB -  L2*sinA*sinB + L1*cosA*One;
 Za_o2 = L2*sinA*cosB +  L2*cosA*sinB + L1*sinA*One;
 
 for i = 1:len;
	plot(Ya_o2(i,:),Za_o2(i,:) );
	hold on;
    pause(0.5); %暂停0.5s
 end

关于欧拉旋转矩阵：https://en.wikipedia.org/wiki/Rotation_formalisms_in_three_dimensions

pdf在百度文库：http://wenku.baidu.com/view/12e8d64b58f5f61fb736668b

========= 用矩阵的理解方式来理解坐标变换 ========

   坐标变换的公式：

   T a_o2  =  T a_o1 * T o1_o2  ？？是这意思么