经历了1周的徘徊,还是强迫自己把LINE的算法继续钻研下去。
困难就是看不懂。坚持看论文和代码,一定要执着地钻研下去。
1. 问题定义
定义1:Information Network:
An information network is defined as $G = (V, E)$ , V是节点集,E是边集。每条边 $e\in E$ 是一个对 $e = (u,v)$ ,还分配了一个权重 $w_{uv} > 0 $用来表示连接的强度。如果G是无向图,我们有$(u,v) \equiv (v,u)$ and $w_{uv} \equiv w_{vu}$ ,如果G是有向图,我们有$(u,v) \not\equiv (v,u)$ and $w_{uv} \not\equiv w_{vu}$ .
定义2:First-order Proximity:
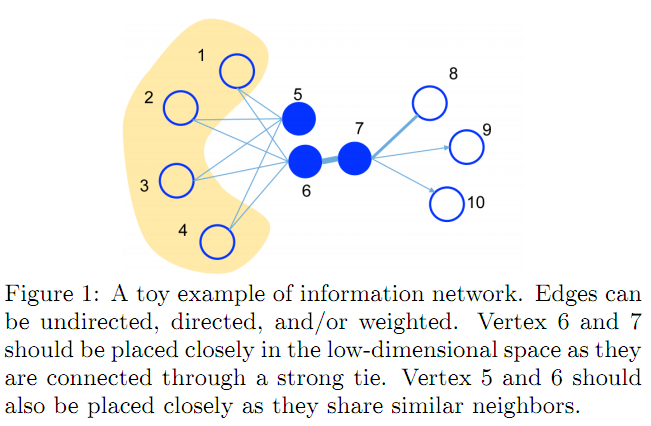
一阶相似度:2个节点的本地相似性,即,对每个连接对,节点被一条边$(u,v)$连接。而这个链接的权重$ w_{uv} $ 就表示了一阶相似度。如果没有连接,那么它们的一阶相似度就为0.
但光有了一阶相似度还不够,比如有的节点之间本来有关系,但它们没有连接,而是通过 share similar neighbors 的方式。所以有了二阶相似度定义。
定义3:Second-order Proximity:
二阶相似度: 一对节点$(u,v)$的二阶相似度是在他们邻居网络上的结构相似性。(关注的邻居网络的结构相似性). Mathematically, let $p_u = ( w_{u,1},w_{u,2}, ... ,w_{u,|V|} )$ 表示了节点$u$ 与其他所有节点的一阶相似度。let $p_v = ( w_{v,1},w_{v,2}, ... ,w_{v,|V|} )$ 表示了节点$v$ 与其他所有节点的一阶相似度。那么,节点$u$和$v$的二阶相似度就决定于$p_u$ 和 $p_v$之间的相似度。如果没有节点既连接$u$又连接$v$,那么$u,v$之间的相似度就为0.
考虑一阶和二阶相似度的网络嵌入,看定义4:网络嵌入
定义4:Network Embedding:
LINE的目的是要: 把大规模网络$G = (V, E)$ 中的节点 $v\in V$ 表示成低维向量空间 $R^d$ ,也就是说,学习一个映射 $f_G:V \to R^d$, 这个 $d \ll |V|$. 在$R^d$空间里,一阶相似性和二阶相似性都能得到保留。
2. 模型构建
一个好的真实信息网络的嵌入模型要有以下特点:
- 能表达一阶二阶相似性
- 能适应每个大的网络,百万级的节点和十亿级的边
- 可以处理任意类型的边:有向,无向,有/无权重。
LINE就可满足上3条要求。
2.1 一阶相似性构建
相似性模型构建的基本思想还是 用带参数θ的模型 Model(θ)去逼近 Empirical Distributions,然后最小化二者之间的距离。
一阶相似性的本质是看2个节点之间是否有边连接。
1)(概率模型 Model) 就是构造出来的模型,用以逼近经验分布。为了构建一阶相似性,对于每个无向边 $(i,j)$ , 我们对节点 $v_i$ 和 节点 $v_j$定义联合概率,如下:
$$ p_1(v_i, v_j) = \frac{1}{1+\mathrm{exp}(-\vec u_i^T \cdot \vec u_j )} \qquad\qquad\qquad(1) $$
这里$\vec u_i \in R^d$ 就是$v_i$节点在$R^d$空间里的低维向量表达。这里公式(1)在空间$V \times V$上定义了一个分布:$p(\centerdot, \centerdot)$
【按】本质上讲,$\vec u_i^T \cdot \vec u_j$ 这个内积衡量了2个节点的一阶相似性,这是一个假设。但若用$-|\vec u_i - \vec u_j|$,向量差,作为相似性是否也可以?(只不过不好求导迭代)是否可以证明用内积表达的向量相似性和用向量差表达的相似性,有何异同?优劣?向量相似性表达方式、评价方式是否会带来实验效果的差异甚至提升?
2)不妨考虑一下这个一阶相似性的经验分布,我们用什么方法来衡量两个节点$(v_i, v_j)$的一阶相似性呢?用$w_{i,j}$吧:
$$ \hat{p}_1(i,j) = \frac{w_{ij}} {\sum_{(i,j)\in E } w_{i,j} } $$
这里分母$W = \sum_{(i,j)\in E } w_{i,j}$ 是否是所有边的权重和?
有了这2种分布表达公式,我们要让向量产生的分布$ p_1(v_i, v_j)$和经验产生的分布$ \hat{p}_1(i,j)$之间的差距最小,如何衡量二者的差距呢?引入一个分布距离$d(\centerdot, \centerdot)$,定义目标函数$O_1$
$$O_1 = d( \hat{p}_1(\cdot,\cdot) , p_1(\cdot,\cdot) ) \qquad\qquad\qquad (2)$$
这只是一个抽象定义,至于具体计算,我们选择K-L散度作为这个距离的计算标准,消去中间过程,得到:
$$ O_1 = -\sum_{(i,j)\in E} w_{ij} \, \mathrm{log } \, p_1 (v_i, v_j) \qquad\qquad\qquad (3) $$
一阶相似性就此刻画。只适用于无向图,不适用于有向图,通过找到这个集合$ \{ \vec {u}_i \} _{i=1,2, ... , |V|} $ 使得(3)式能取得最小值,我们就可把每个节点表达在d维空间中。
【读者按】:由于sigmoid函数$\frac{1}{1+e^{-x}}$和log函数都是单增函数,而$ \vec u_i^T \cdot \vec u_j = |\vec u_i| |\vec u_j| cos(\theta) $ ,$ \theta $是向量夹角。可分析知,$O_1$ 中的每一项,实质上是当向量 $ \vec u_i$ 和 $ \vec u_j $ 内积最小时,$O_1$取得最小。当节点间的权重$w_{ij}$越大,越要使其向量表达的内积小,才能取得$O_1$的最小值。
2.2 二阶相似性构建
为了构建二阶相似性,同样需要构造一个理论分布,一个经验分布,以及二者的距离。
二阶相似性是同时适用于有向图和无向图,先假设是有向的,(无向图看成是双向有向图),二阶相似性是基于一个假设:两个节点share的其他节点越多,认为是二阶相似性越大。
每个节点看成是一个特别的context,对于节点来说,如果两个节点share更相似的context,那么假设它俩的二阶相似性更高。
那么每个节点其实充当了2个角色:节点本身,和,别的节点的上下文。相当于一个人的2个角色:自我角色和他我角色。做自己,也要做别人眼中的他人。
对每个节点引入2个向量:$\vec u_i$ 和 $\vec u_i'$。其中,$\vec u_i$ 用来表达节点本身,而当节点$i$被视作context时,用$\vec u_i'$ 来表达。
1. 经验分布(w,V,E), $\hat p_2 (\cdot , v_i) $
经验分布是要展现一个条件概率,条件是节点$i$出现,求它的上下文出现的概率。
经验分布 $\hat p_2 (\cdot , v_i) $ 表达式:
$$\hat p_2 (v_j | v_i) = \frac{w_{ij}}{ \large{\sum }_ {k \in N(i)} w_{ik} } $$
- $w_{ij}$ 是有向边$(i,j)$的权重
- 分母是节点i的出度。文章里记作$d_i = \sum_{k \in N(i)} w_{ik}$
- $N(i)$ 是节点$v_i$的外邻居(out-neighbors)
经验分布 $\hat p_2 (\cdot , v_i) $ 其本质是一个条件分布,意义在于,在节点$v_i$出现的条件下,其上下文 $v_j$出现的概率。节点$i$可能同时指向多个节点,所以其指向节点$j$的条件概率就是上面的分数形式。
2. 模型分布, 理论分布:(概率模型 Model) 就是构造出来的模型,用以逼近经验分布。
模型分布的设计思想:对一个有向边$(i,j)$,节点i生成上下文j的概率:
从节点i出发,对所有与它相连的节点进行遍历,即向量$u_i$与所有别的节点的context向量 $\vec u_k'$ 作内积。再看$u_i$与节点j的context的向量$\vec u_j’$的内积的占比。作为i,j 节点的二阶相似性。
$$p_2(v_j|v_i) = \frac{\mathrm{exp}(\vec u_j'^T \cdot \vec u_i )}{\sum_{k=1}^{|V|} \mathrm {exp} (\vec u_k'^T \cdot \vec u_i )} \qquad\qquad\qquad (4) $$
公式中,$|V|$是i的context的数量或节点数量。对于每个节点$v_i$,公式4实际上定义了一个在上下文(也即是全部节点集)上的条件分布$p_2(\cdot | v_i)$。注意$\hat p_2$的经验分布里,$k\in N(i)$ 是仅考察与$i$有出边连接的节点集$N(i)$, 而对于模型分布 $p_2(\cdot | v_i) $, 由于不知$v_k$与$v_i$是否有边,只能取所有的$v_k$, $k \in \{1,2,...,|V| \} $
二阶相似性假设:在context上的分布相似的节点认为是二阶相似性更大的。
【按】:这里模型分布是利用每个节点的2种向量来计算节点$i$出现时,节点$j$出现的条件概率,而用公式(4)这样的方式表达这个条件分布,实际是利用向量内积表达节点$i$的context出现的可能性。这种方式是否合理呢?要看语言模型里,$p(\text{context}|x)$是如何用词向量表达的。以及如何借助其训练机制,即与语言模型类似,context可能性太多,训练时需要使用简化方法。
3. 距离:也就是目标函数
$$O_2 = \sum_{i\in V} \lambda_i d(\hat p_2(\cdot, v_i) , p_2(\cdot, v_i) ) \qquad\qquad\qquad (5) $$
对于每个节点$v_i$,都分配了一个权重$\lambda _i$,然后用距离函数$d(\cdot, \cdot)$计算对于每个节点$v_i$的经验分布$\hat p_2(\cdot, v_i)$和模型分布$p_2(\cdot, v_i) $的距离。最后加权求和。至于权重$\lambda _i$,可用度数或者PageRank类似算法获得。本文就用的 节点$v_i$的出度$d_i$来表示$\lambda _i$,$d_i = \lambda _i$。
通过约减常数项,整理后得到:
$$ O_2 = -\sum_{(i,j)\in E} w_{ij} \mathrm{log}\,p_2(v_j, v_i) \qquad\qquad\qquad (6) $$
通过学习$\{ \vec u_i\}_{i=1,2, ... , |V|}$ 和 $\{ \vec u_i'\}_{i=1,2, ... , |V|}$ 使得 $O_2$ 取得最小,我们可以得到节点$v_i$的向量表达$\vec u_i$。
至此,完成文档的第一部分,基本模型构建过程。这里有几个问题:
- 二阶相似性里,利用向量内积表达节点同时出现的可能性,是否合理?
- 语言模型里,$p(\text{context}|x)$是如何用词向量表达的?
- 语言模型训练的简化方法:Negative Sampling究竟是如何工作的。
3. 模型优化
3.1 负采样公式及其粗浅理解
优化公式(6)计算量太大。原因是计算条件概率$p_2(\cdot | v_i)$时,分母要对所有的节点进行运算求和。这里我们采用的nagative sampling. 对每一条边$(i,j)$根据某种噪声分布采样几个nagative edges。更特殊地,对每一条边,它用了下面的目标函数:
$$ \mathrm{log} \, \sigma (\vec u_j'^T \cdot \vec u_i) + \sum_{i=1}^{K} E_{v_n \thicksim P_n(v)}[\mathrm{log} \, \sigma(-\vec u_n'^T \cdot \vec u_i)] \qquad\qquad (7)$$
这个目标函数,$\sigma(x) = \frac{1}{1+e^{-x}}$ 是sigmoid函数。
‘$+$’ 号前部分$ \mathrm{log} \, \sigma (\vec u_j'^T \cdot \vec u_i)$是节点$(i,j)$的向量之间的计算,文章中称是建模了观察到的边。
‘$+$’ 号后部分$\sum_{i=1}^{K} E_{v_n \thicksim P_n(v)}[\mathrm{log} \, \sigma(-\vec u_n'^T \cdot \vec u_i)]$是采样一部分节点,文章中称是从噪声分布中采样得到的负样本的边。其中,$K$是负样本边的个数。这里有个节点$v$ ,记节点$v$的出度为$d_v$,有$P_n(v) \varpropto d_v^{\frac{3}{4}}$.
【按】
- 在word2vec中,负样本是给定一个词$w$,生成$NEG(w) $,$NEG(w) $是未与词$w$搭配的词$\tilde {w}$的集合,再采样后构成的集合。
- 这里的负样本是什么?是对于节点$v_i$,未与之产生边的节点集合(即未成为节点$v_i$的context),的采样集$NEG\{ (i,j)\} $——负样本节点集。
- 文章说,$K$是负样本边的个数($K$ is the number of negative edges)。什么叫negative edges,我认为是$v_i$与本与之没有边的节点$v_n$之间的假想边,就像无法成对出现的$w$与$\tilde {w} $单词对一样。
- 这里本质上是要训练一个二分类器,既然是二分类器,就要有正样本和负样本用于训练模型。
- 一个节点在语言模型中相当于一个词$w$,而语言模型中,一个词$w$会在语料$\mathcal{C}$中出现多次。对应网络中,可假设一个节点被多条边占用,故在边集$E$中,节点$v$可出现多次。因此,一个节点的出度$d_v$对应了一个词$w$的频度,在word2vec模型中,记作$\mathrm{counter}(w)$。所以在此,有$P_n(v) \varpropto d_v^{\frac{3}{4}}$。
- 公式7中,$E_{v_n \thicksim P_n(v)}$,目前理解,就是负采样后得到的负样本边集。由于$(-\vec u_n'^T \cdot \vec u_i)$的括号里有个负号,故整个优化是最大化正样本概率。
- 相当于公式$(7)$的第一项是考虑的正例的概率,第二项考虑的负例的概率,让正例的概率足够大而负例的概率足够小,即是公式$(7)$的优化目标。
- 此处还是基于一个假设,即,$ \mathrm{log} \, \sigma (\vec u_j'^T \cdot \vec u_i)$用以表达节点$i$和节点$j$之间的的联系。类似词$w_i$的上下文是$w_j$. 这里是否值得推敲?
3.2 目标函数$O_1$的优化
对于目标函数(3),
$$ O_1 = -\sum_{(i,j)\in E} w_{ij} \mathrm{log} \frac{1}{1+\mathrm{exp}(-\vec u_i^T \cdot \vec u_j)}$$
有个不重要的解(trivial solution):$u_{ik} = \infty $, for $i=1,2,...,|V|$ and $k=1,2,...,d$.为了避免这种情况,我们将公式(7)中的$\vec u_j'^T $ 替换成 $\vec u_j^T$即可。
3.3 目标函数公式(7)的优化
对于公式(7),使用ASGD(asynchronous stochastic gradient),异步随机梯度算法进行优化,在每一步,ASGD算法采样一个小批量边,然后更新模型的参数。
如果一条边$(i,j)$被采样到,关于节点$v_i$的嵌入向量$\vec u_i$的梯度,将按照下式计算:
$$ \frac{\partial O_2}{\partial \vec u_i} = w_{ij} \cdot \frac {\partial \, \mathrm{log} \, p_2(v_j|v_i)}{\partial \vec u_i} \qquad\qquad (8)$$
注意边的权重$w_{ij}$要乘进去。但当$w_{ij}$方差比较大时,这里就会有问题。例如,在一个单词occurrence网络里,有的单词对出现几万次,但有的只出现几次。这种网络里,梯度的scales 偏离,而且很难选择一个合适的学习率。如果我们按照小权重边选择了大的学习率,大权重边上的梯度就会爆炸;如果我们为大的权重边选择了小的学习率,又会遇到收敛太慢的问题。
3.4 边采样EdgeSampling
为了解决上述问题,可以将有权边缘展开为多个无权边,例如,具有权重$w$的边展开为$w$个无权边。但是展开后,会显著增加内存需求。解决方案为:现在网络中,对边进行采样,采样的概率与边的权重成正比;再将采样后的边展开成无权边。这样就可以找到合适的学习率,并且不需要修改目标函数。那么,如何根据权重在网络中对边进行采样呢?LINE采用了别名抽样法。
令$W=(w_1,w_2,...,w_{|E|},)$是边权重序列。$ w_{sum} = \sum_{i=1}^{|E| w_i}, 在区间$[0,w_{sum}]$中等概率随机取一个数,这个数落在一个区间$[\sum_{j=0}^{i}w_j,\sum_{j=0}^{i}w_j]$中,此时的$i$就是采样到的边编号,从而取$w_i$作为样本。然后文章讨论了计算时间复杂度,这里不作重点。引用一段:
通过别名抽样法采样一个边需要的时间为$O(1)$;负采样的优化需要$O[d(K + 1)]$时间,其中$K$是负样本的数量。因此,总体上每个步骤需要$O(dK)$时间。在实践中,发现用于优化的步数通常与边$O(| E |)$成正比。因此,LINE的整体时间复杂度为$O(dK | E |)$,它与边数$| E |$成线性关系,并且不依赖于顶点数$| V |$。
作者:玛卡瑞纳_a63b
链接:https://www.jianshu.com/p/8bb4cd0df840
來源:简书
4. 一些问题的讨论
在LINE模型里还有些实操的问题,如:
这样的节点的邻居数量非常少,所以很难精确地推断它的表示,特别是基于二阶相似度的方法(很依赖context)。解决方案是通过添加更高阶的邻居扩展这些顶点的邻居,例如将节点邻居的邻居作为节点的邻居。LINE中只考虑向每个顶点添加二阶邻居,即邻居的邻居。顶点$i$与其二阶邻居$j$之间的权重被测量为:
新加入的顶点如何处理?
1.新加入节点$i$与已有节点的连接已知的情况:可以在已有的节点基础上,得到经验分布$\hat p_1(\cdot|v_i)$和$\hat p_2(\cdot | v_i)$,然后可以根据目标函数(3)或目标函数(6),通过最小化下面的任一目标函数得到新节点的向量表示(已有节点的向量表示保持不变)
$$-\sum_{j\in N(i)} w_{ji} \mathrm{log} \, p_1 (v_j, v_i) = -\sum_{j\in N(i)} w_{ji} \mathrm{log} \frac{1}{1+\mathrm{exp}(-\vec u_j^T \cdot \vec u_i )}$$
或:
$$-\sum_{j\in N(i)} w_{ji} \mathrm{log} \, p_2 (v_j | v_i) = -\sum_{j\in N(i)} w_{ji} \mathrm{log} \,\frac{\mathrm{exp}(\vec u_j'^T \cdot \vec u_i )}{\sum_{k=1}^{|V|} \mathrm {exp} (\vec u_k'^T \cdot \vec u_i )}$$
2. 新加入节点i与已有节点的连接未知的情况:需要根据新节点的其他信息,如新节点的文本信息,LINE中没有实现。"Leave as our future work."
5. 实验设计
参考简书上的总结(https://www.jianshu.com/p/8bb4cd0df840)[https://www.jianshu.com/p/8bb4cd0df840]即可。
【我想说的是】:实验分析里有很多干货,值得细细研读。