问题背景:在大量文本中,对每个单词的出现次数进行统计,可以得到一张单词出现次数的表格。如:
| word | #existance | #of word with same existance |
|---|---|---|
| a | 100,000 | 20 |
| an | 100,000 | 20 |
| boy | 99,888 | 19 |
| cat | 99,877 | 18 |
| … | … | … |
| dog | 5000 | 3000 |
| eat | 4000 | 3000 |
| … | … | … |
| folkloristic | 20 | 80000 |
| wacky | 10 | 80000 |
| zannichelliaceae | 1 | 90009 |
后面2列,可据此形成二维坐标中的某个点。比如出现次数为100,000的单词,有20个。则对应坐标的横轴100,000,纵轴20.
将所有的行都在坐标中标注,并去掉重复的标注点,即可得到如下的图:
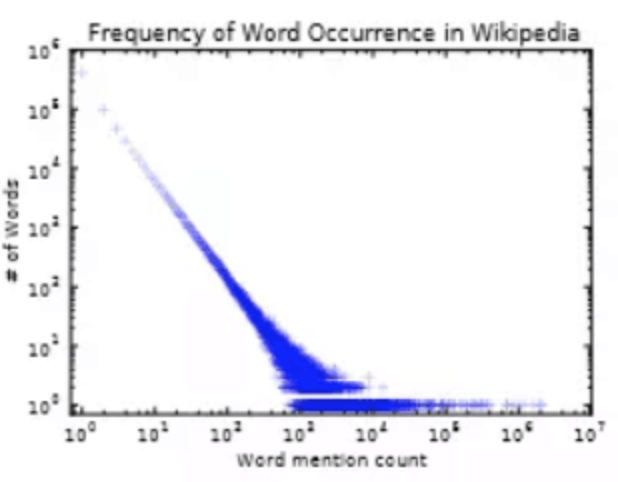
文本中的幂率分布即如下现象:
可以看到具有低出现次数的单词(横坐标较小),数量很大(纵坐标较大)。反之,具有高出现次数的单词,比如a, of, with, for … 数量并不多。而且在幂坐标系里,基本呈现线性,这就是所谓的幂率分布。
可看成是一排学生,出现的次数相当于学生的身高。那些身高很高的学生个数并不多,而身高不高的学生数量庞大。大量单词仅仅出现少量的几次。
对于Random Walk爬取的context, 其节点出现的频率与具有此频率的节点个数之间,也服从类似word 的幂率分布,这是DeepWalk拿来说事儿的根基。如图:
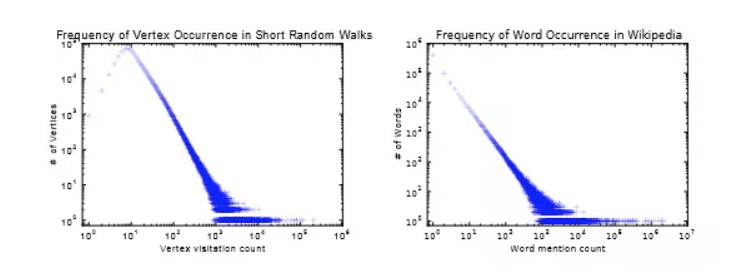 。
。
网络节点的度分布与power law
看一个netGAN 论文(ICML2018)中的图:
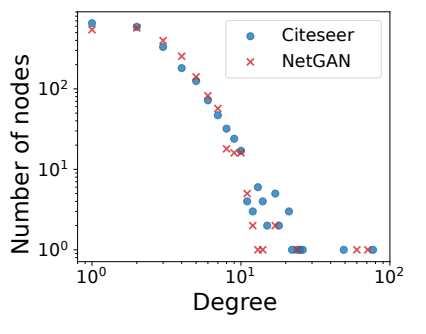
度数小的节点,位于x轴左侧,数量较大,y轴上侧。度数大的节点,位于x轴右侧,在y轴上处于值较小的位置,及数量较少。